
Today, we'd like to honour Princeton mathematician John Conway, who passed away from COVID-19 at 82 years old. He made impressive contributions in various areas of mathematics but is most widely known for his invention of Conway's Game of Life, a cellular automaton in which simple rules give rise to surprisingly complex behaviours.
The rules couldn't be simpler. You start with an infinite grid of square cells that can be either black or white (metaphorically, alive or dead). At each second update, the colour of each cell, depending on the state of its eight neighbours (horizontally, vertically, or diagonally adjacent cells), will change:
- Any live cell with fewer than two live neighbours dies, as if by underpopulation.
- Any live cell with two or three live neighbours lives on to the next generation.
- Any live cell with more than three live neighbours dies, as if by overpopulation.
- Any dead cell with exactly three live neighbours becomes a live cell, as if by reproduction.
With just these rules, we can observe the following common patterns:
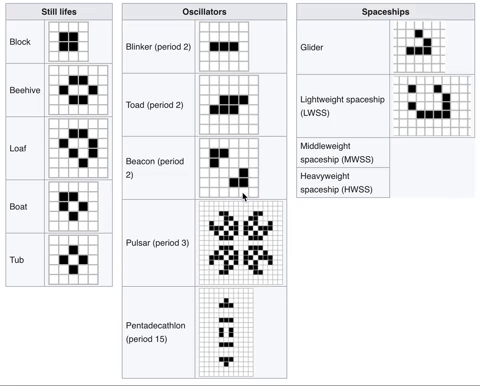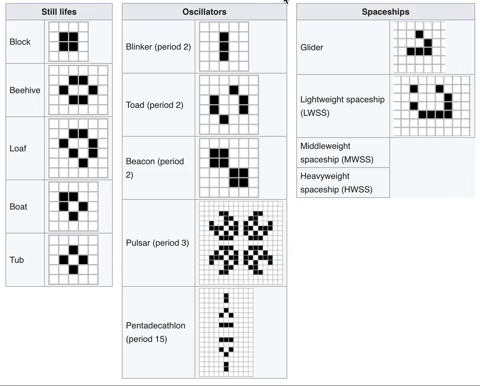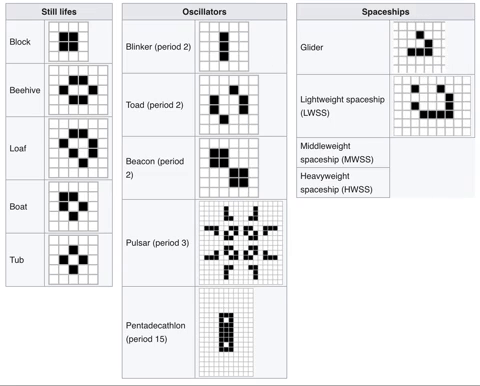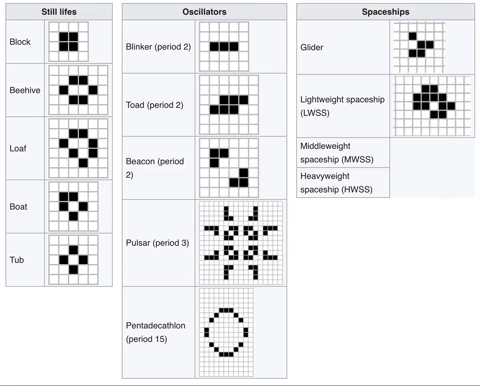
Despite its simplicity, different starting patterns can simulate interesting behaviours like emergence, self-organization and self-replication—behaviours that we associate with complex systems and biological processes. Evolving Web's logo is a stylized form of the Glider, a five-square pattern that maintains its shape while moving across the grid. There's also a glider gun, a pattern that generates an infinite amount of such gliders.
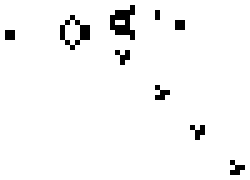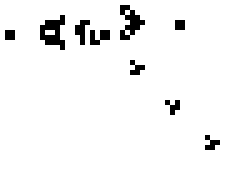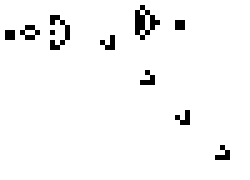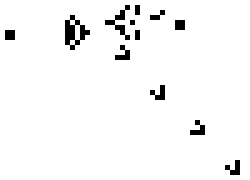
Algorithmically, Conway's Game of Life has the power of a universal Turing machine: any calculation that can be computed algorithmically can be simulated with the right arrangement of cells. But in human terms, the real universality of the Game of Life is its suggestion that the apparently infinite complexities we see in the world around us might be explained by repeated iteration of just a few simple rules. It's this universality that inspired us to use the Glider as Evolving Web's logo.
Conway’s genius led to many discoveries and accomplishments far deeper and more fundamental than the Game of Life, in the fields of group theory, number theory, algebra, geometric topology, theoretical physics, combinatorial game theory and geometry. The achievement Conway himself was most proud of was his invention of a new system of numbers, the surreal numbers. This continuum of numbers includes not only real numbers such as integers, fractions and irrational numbers such as pi, but also the infinitesimal and infinite numbers. (Source: princeton.edu)
To learn more about John Conway's life and work, see the obituary published by Princeton University.


